Herman Minkowski – A Great Educator makes a Great personality.

Hermann Minkowski was a mathematics teacher to Albert Einstein at the Eidgenössische Polytechnikum, which is now ETH Zurich. Minkowski was a mathematician who taught at universities in Bonn, Königsberg, Zürich, and Göttingen. He died of appendicitis in 1909 at the age of 44. Minkowski’s work provided the mathematical foundation for Einstein’s general theory of relativity. In 1908, Minkowski explained the geometric structure of Einstein’s special theory of relativity in a speech at the 80th Assembly of German Natural Scientists and Physicians. Today, physicists still use Minkowski’s work. 

• He developed the geometrical theory of numbers and made numerous contributions to number theory, mathematical physics, and the theory of relativity
• Minkowski space or spacetime is used in mathematical physics and special relativity. It combines 3-dimensional Euclidean Space and time into a 4-dimensional manifold, where the interval of spacetime that exists between any two events is not dependent on the inertial frame of reference.

What Is Minkowski Space?

Minkowski space or spacetime is used in mathematical physics and special relativity. It combines 3-dimensional Euclidean Space and time into a 4-dimensional manifold, where the spacetime interval between any two events is not dependent on the inertial frame of reference. This concept was initially developed by the Scientist Hermann Minkowski for Maxwell’s equation of electromagnetism.

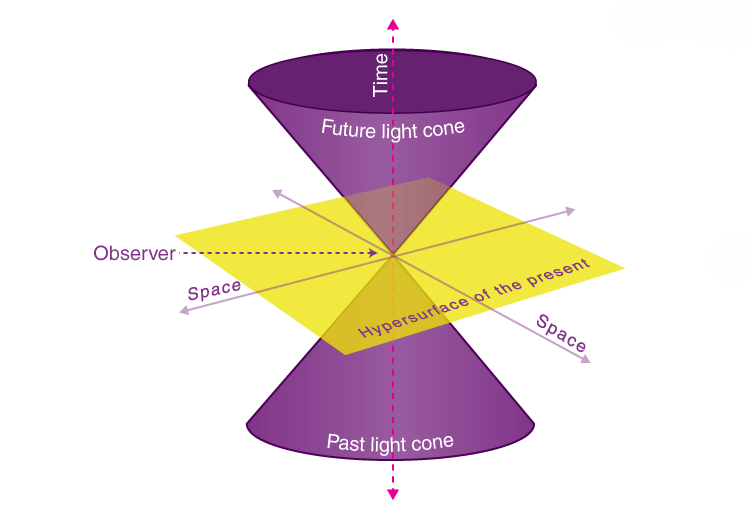
The mathematical structure of Minkowski spacetime was an immediate consequence of the postulates of relativity. The individual components in Euclidean space and time vary due to time dilation and length contraction. All the reference frames in Minkowski spacetime agree on the spacetime’s overall distance between the events. This is because it treats the 4th dimension (time) differently than the three spatial dimensions. The metric signature of Minkowski spacetime is represented as (-+++) or (+—), and it is always flat.

Mathematical Definition

Minkowski spacetime is a 4-dimensional coordinate system in which the axes are given by (x, y, z, ct)

We can also write as (x¹, x², x³, x⁴).

Here we have written ct as x⁴, time is measured in units of speed of light times the time coordinates this is because the unit of time should be same as the unit for space.

The differential for arc length in spacetime is given by the equation:

This equation has a metric tensor of spacetime given by:

guv=[−1000010000100001]

As stated before, spacetime is a flat everywhere.

Minkowski Diagrams

The scientist used a separate graphing system called Minkowski diagrams to properly demonstrate the properties of Lorentz transformation and relate the Newtonian mechanics to relativistic mechanics using proper graphical methods.

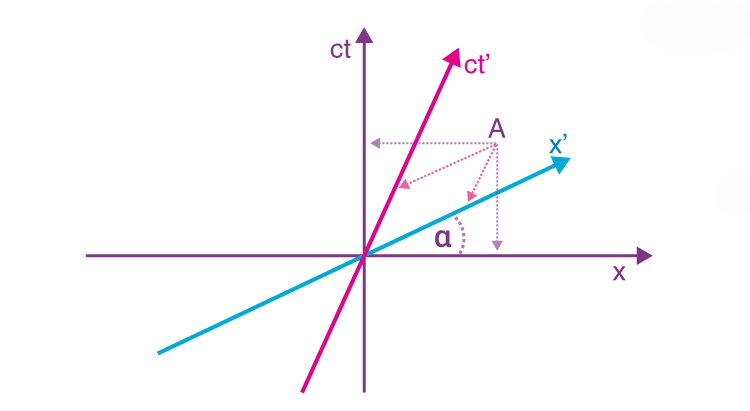
As you see in the image, different coordinate systems will not agree on the object’s position or spatial orientation in time. We can see that there is one spatial axis, i.e. x-axis, and the other is the time axis, i.e. ct-axis.

The Minkowski Spacetime has a different set of rules for graphing, which are as follows:

1. tanΘ=vcis the angle between the x-axis and x`-axis where ‘v’ is the object’s velocity.
2. The speed of light in the spacetime always makes an angle of 45° with either axis.

Interested to learn more about related topics, below are the links:

• difference between the equinox and solstice
• equivlance principle

Minkowski Space in General Relativity

Einstein used the following equation in the general theory of relativity

This equation allows the spacetime to actually curve the resulting effects are those of gravity.

Have you ever wondered why objects fall? What is this force that pulls them towards the earth? How does it work? Watch the video to find answers to all these questions.

Author: Master Vikrant RohinMaster Vikrant Rohin is an international author, and more than four countries’ schools are using his books in the core curriculum of education. He is the author of twenty different subject books. History, Economics, Chemistry, Physics, English, Biology, Geography etc. Most of his students hold high-ranking positions in the public and private sectors. He has cracked the world’s toughest exam, the "Civil Services Examination (UPSC)," eight times. Always a topper in academics, he was also a top-class sportsman, a state boxer, and a basketball player.