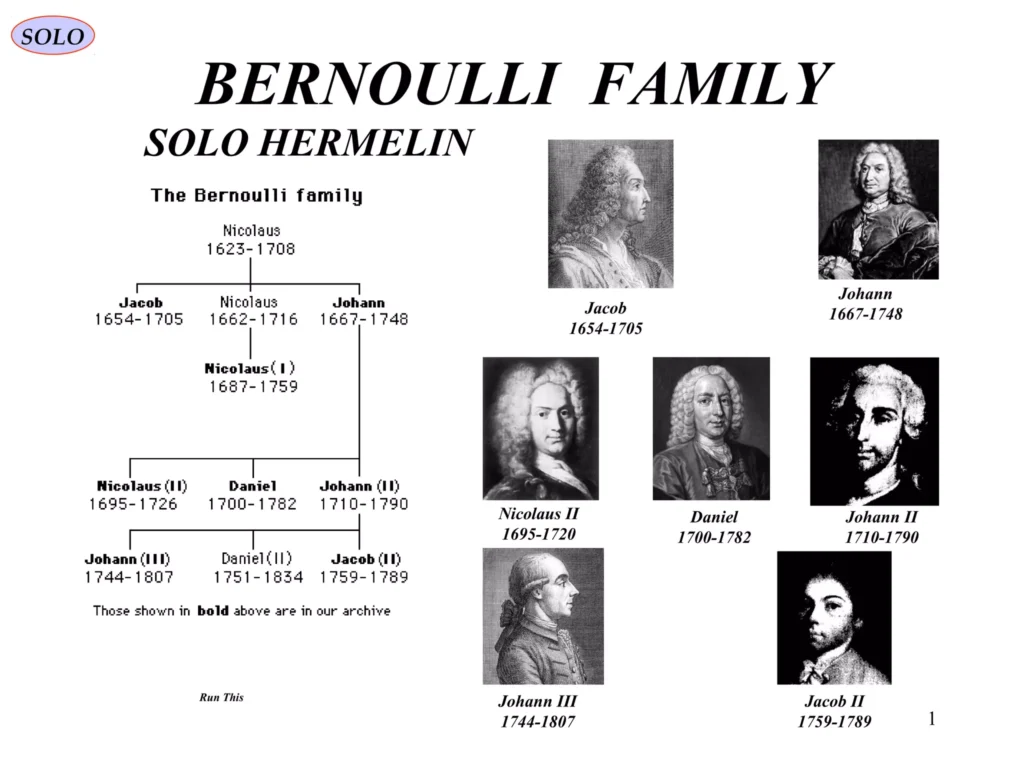
The Swiss mathematician John Bernoulli posed the problem of the brachistochrone(‘shortest time’), to the readers of Acta Eruuditorium in June, 1696. He said:
- I, Johann Bernoulli, address the most brilliant mathematicians in the world. Nothing is more attractive to intelligent people than an honest, challenging problem, whose possible solution will bestow fame and remain as a lasting monument. Following the example set by Pascal, Fermat, etc., I hope to gain the gratitude of the whole scientific community by placing before the finest mathematicians of our time a problem which will test their methods and the strength of their intellect. If someone communicates to me the solution of the proposed problem, I shall publicly declare him worthy of praise
John Bernoulli statement:
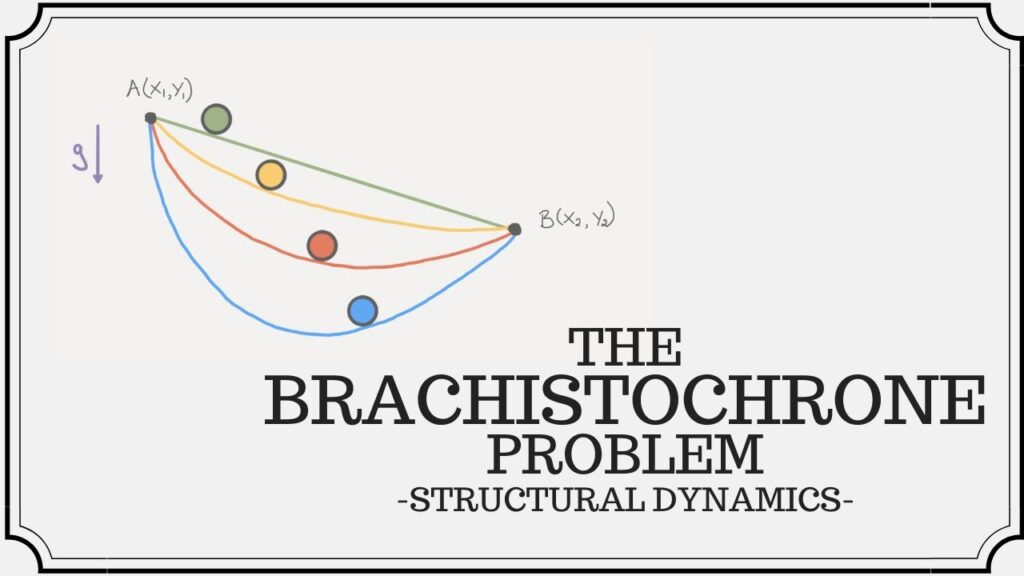
- “Given two points A and B in a vertical plane, what is the curve traced out by a point acted on only by gravity, which starts at A and reaches B in the shortest time?”
- Johann and his brother Jacob Bernoulli derived the same solution, but Johann’s derivation was incorrect, and he tried to pass off Jakob’s solution as his own. And then he challenged the greatest mathematician in Europe, Isaac Newton, to solve it within six months.
On January 29, 1697, at 4 p.m., when Sir Isaac Newton arrived home from the Royal Mint, he found the challenge (Brachistochrone Problem) in a letter .
- The Swiss mathematician Bernoulli had challenged his colleagues to solve it within six months.
- Newton not only solved the problem before going to bed that same night, but in doing so, invented a new branch of mathematics called the calculus of variations.
- He had resolved the issue of specifying the curve connecting two points displayed from each other laterally, along which a body, acted upon only by gravity, would fall in the shortest time.
- Newton, age 55, sent the solution to be published, at his request, anonymously. But the brilliant originality of the work betrayed his identity, for when Bernoulli saw the solution he commented, “We recognize the lion by his claw.”
Brachistochrone curve
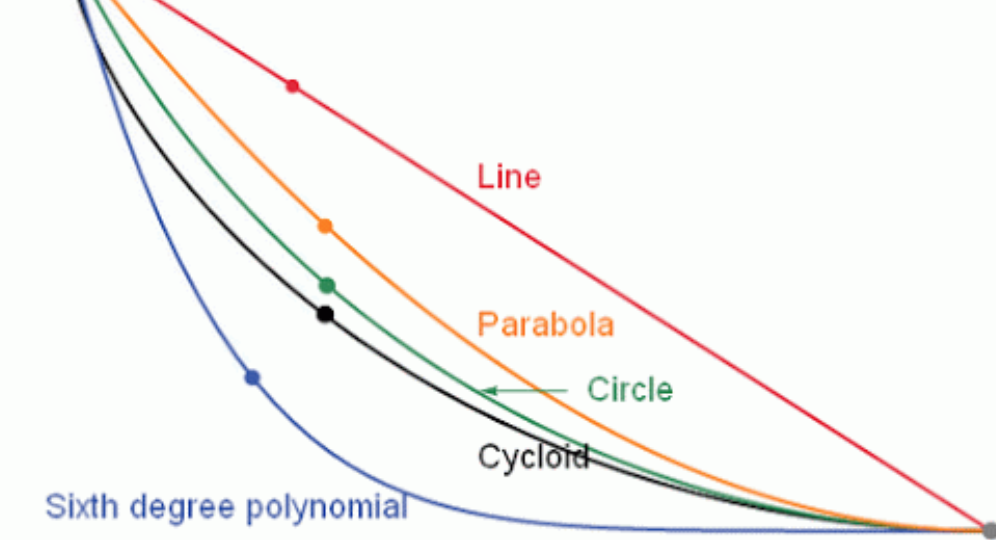
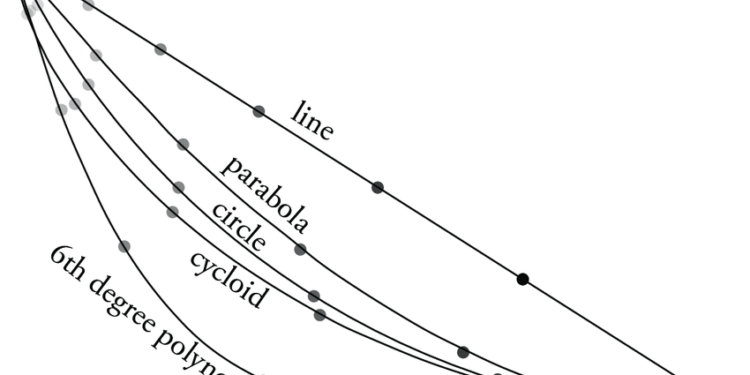
- In physics and mathematics, a brachistochrone curve or curve of fastest descent, is the one lying on the plane between a point A and a lower point B, where B is not directly below A, on which a bead slides frictionless under the influence of a uniform gravitational field to a given end point in the shortest time. The problem was posed by Johnn Bernoulli in 1696.
- The brachistochrone curve is the same shape as the tautichrone curve; both are Cyloids. However, the portion of the cycloid used for each of the two varies. More specifically, the brachistochrone can use up to a complete rotation of the cycloid (at the limit when A and B are at the same level), but always starts at a cusp. In contrast, the tautochrone problem can use only up to the first half rotation, and always ends at the horizontal
The Brachistochrone
- A classic example of the calculus of variations is to find the brachistochrone, defined as that smooth curve joining two points A and B (not underneath one another) along which a particle will slide from A to B under gravity in the fastest possible time.
- Using the coordinate system illustrated, we can use conservation of energy to obtain the velocity v of the particle as it makes its descent


Definition 5 This curve is called a cycloid.The constant α is determined implicitly by the remaining boundary condition y(h) = a. The equation of the cycloid is often given in the following parametric form (which can be obtained from the substitution in the integral)
| x(θ) | = | ||
| y(θ) | = |
and can be constructed by following the locus of the initial point of contact when a circle of radius α/2 is rolled (an angle 2θ) along a straight line.